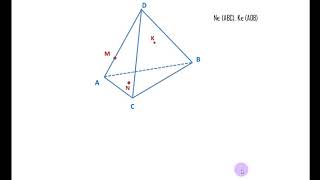
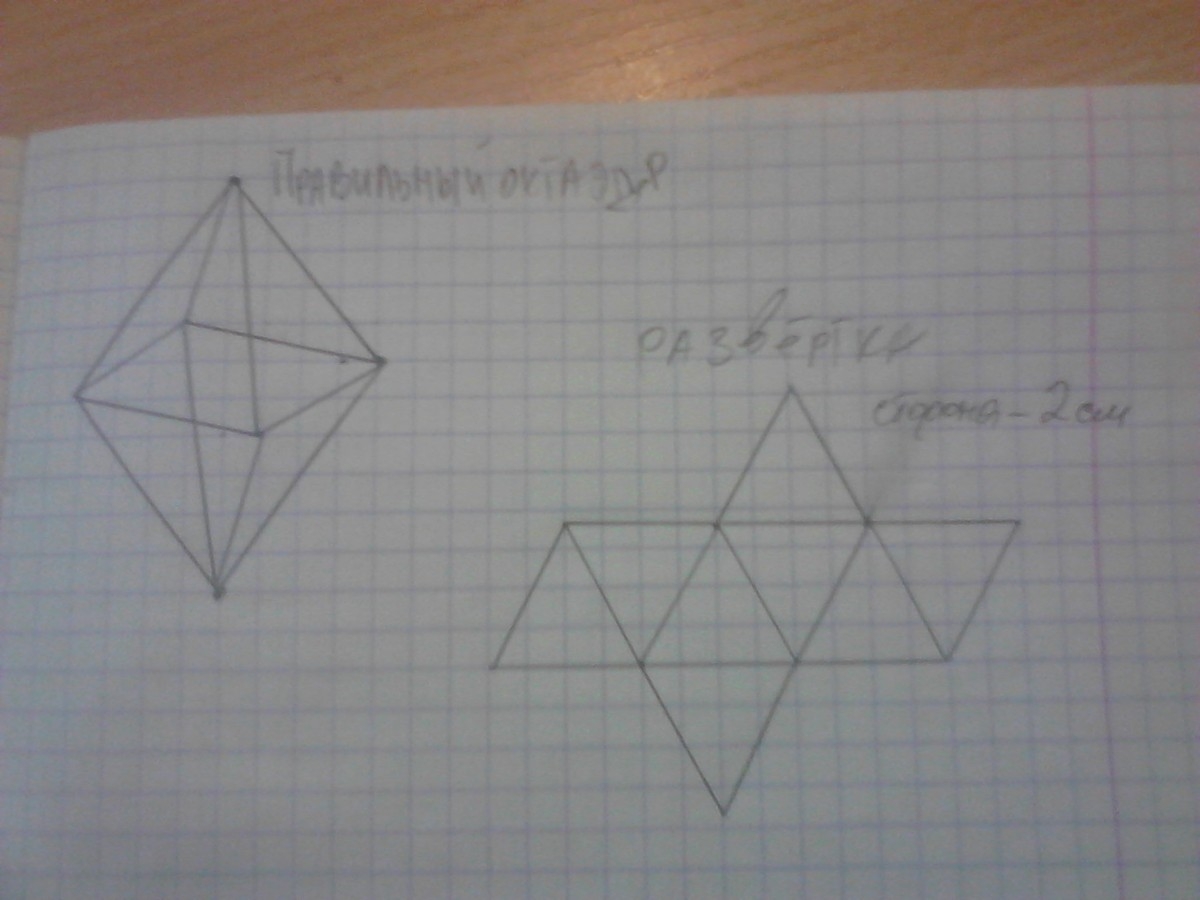
Как нарисовать тетраэдр

Пока на ум пришел немного "костыльный способ". Затем строим плоскость через 3 точки - одна верхняя и 2 нижние любые как на скриншоте:. Если есть возможность, иллюстрируйте свое предложение скриншотами процесса. Или может скринкаст даже.

Красивые узоры по клеточкам

Представляем вам узоры по клеточкам, которые сможет нарисовать любой с помощью обычной тетрадки и нескольких ручек или карандашей. Рисование с помощью сетки из клеток — это один из способов изображения, который отлично подходит для тех, кто хочет научиться рисовать. Попробуйте сами срисовать несколько узоров, и вы поймете, насколько это легко. Художественные способности — это важная часть саморазвития любого человека.

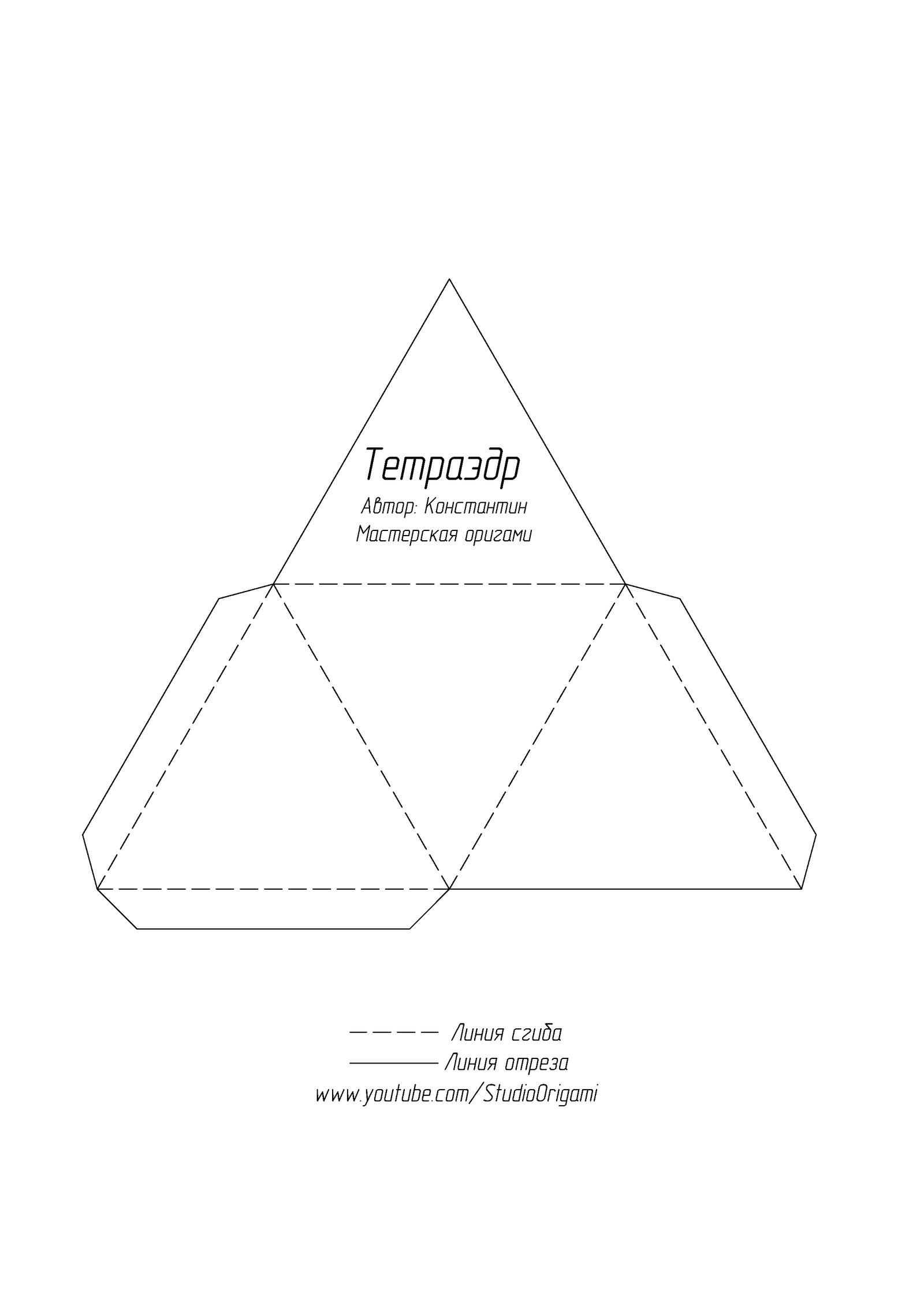
Все сервисы Хабра. Andrei1penguin1 Andrei1penguin1. Как можно это сделать? Тетраэдр должен получиться математически ровным и быть правильным. Подписаться 1 Простой 1 комментарий Facebook Вконтакте Twitter.

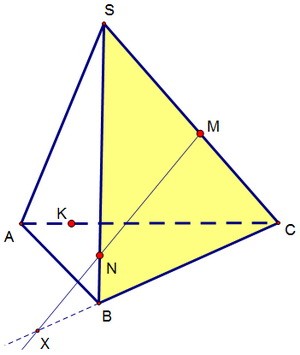
	7	В статье применяется механизм смешивания цветов, позволяющий рисовать полупрозрачные поверхности, а на сцену добавляется тетраэдр. Полупрозрачные тела частично пропускают свет насквозь.
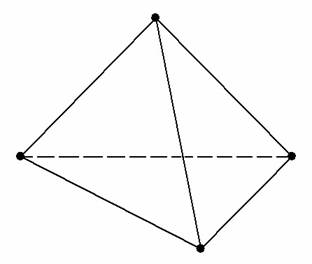
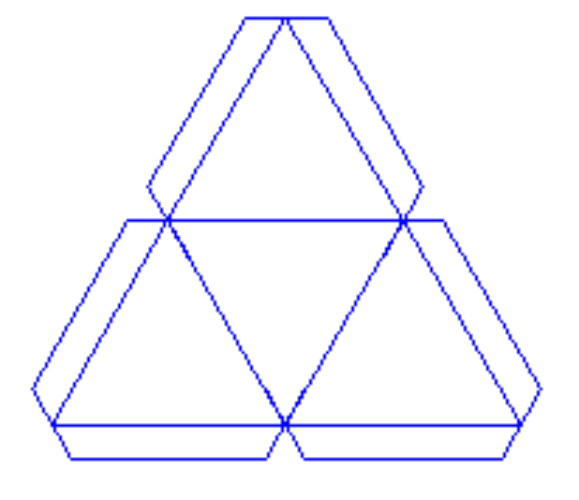
	102	Тетраэдр - это геометрическая фигура, состоящая из четырех треугольников, объединенных в одну точку.
	378	Тетраэдр треугольная пирамида, четырёхгранник — это простейший многогранник, гранями которого являются четыре правильных треугольника.
	16	Регистрация Вход. Ответы Mail.
	73	Ваш e-mail не будет опубликован. Leave this field empty.
	417	Этюды Модели Миниатюры iMath Лекции.
	63	Помагите пожайлуста со следующим заданием: Нарисовать тетраэдр с помощью поворота одного равностороннего треуголнька и векторы нормали ко всем его граням и вершинам.
	266	Прежде чем перейти к основной теме параграфа, рассмотрим несколько подготовительных задач на пересечение. Рассмотрим некоторые случаи их взаимного расположения и построим пересечение:.
	410	Тетраэдр треугольная пирамида, четырёхгранник — это простейший многогранник, гранями которого являются четыре правильных треугольника.

По числу углов основания различают пирамиды треугольные тетраэдр , четырёхугольные и т. Пирамида является частным случаем конуса [2]. Начало геометрии пирамиды было положено в Древнем Египте и Вавилоне , однако активное развитие получило в Древней Греции. Объём пирамиды был известен древним египтянам.