Свойства связанные с биссектрисами треугольника

Свойства биссектрисы угла
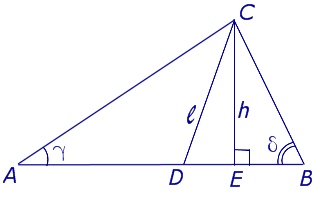
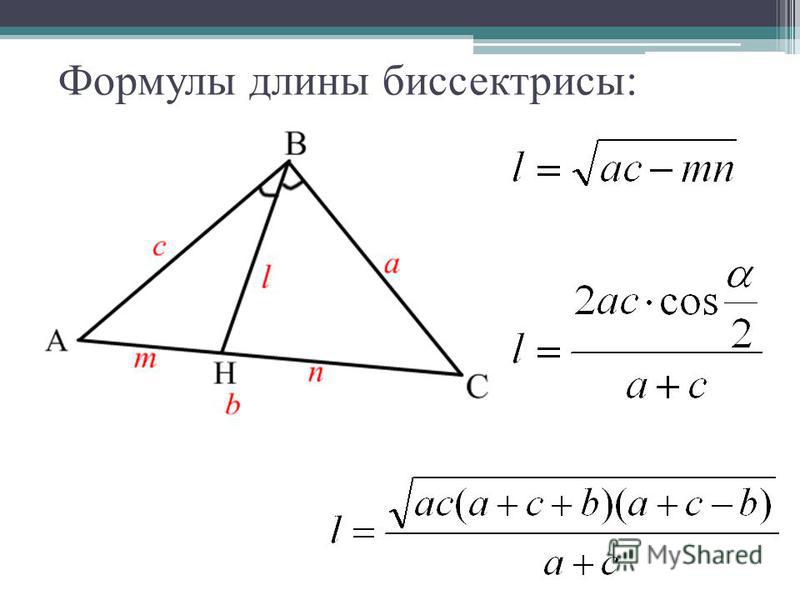
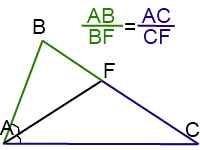
Теорема о биссектрисе — классическая теорема геометрии треугольника. Биссектриса при вершине треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам. Теорема о биссектрисе формулируется в шестой книге « Начал Евклида » предложение III [1] , в частности, на греческом языке в византийском манускрипте [2]. Существует несколько методов доказательства. Например, методом площадей или проведением из другой вершины прямой, параллельной биссектрисе, до ее пересечения с продолжением одной из сторон. Рассмотрим треугольник ABC.
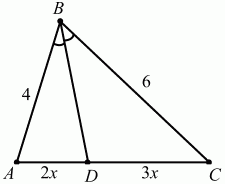

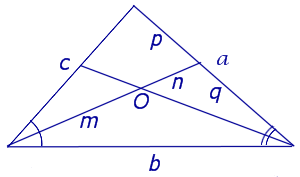




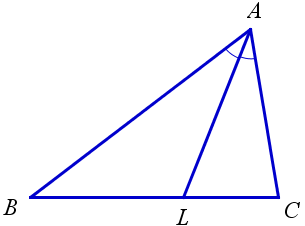
Попробуйте повторить позже. Докажите, что биссектриса треугольника делит его сторону на отрезки, пропорциональные двум другим сторонам. Проведем через точку прямую Тогда как накрест лежащие, образованные параллельными прямыми и и секущей Также как соответственные, образованные параллельными прямыми и и секущей. Таким образом, — равнобедренный, то есть. Рассмотрим треугольник и его биссектрису.
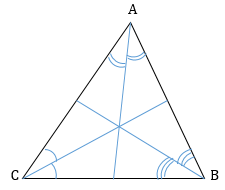
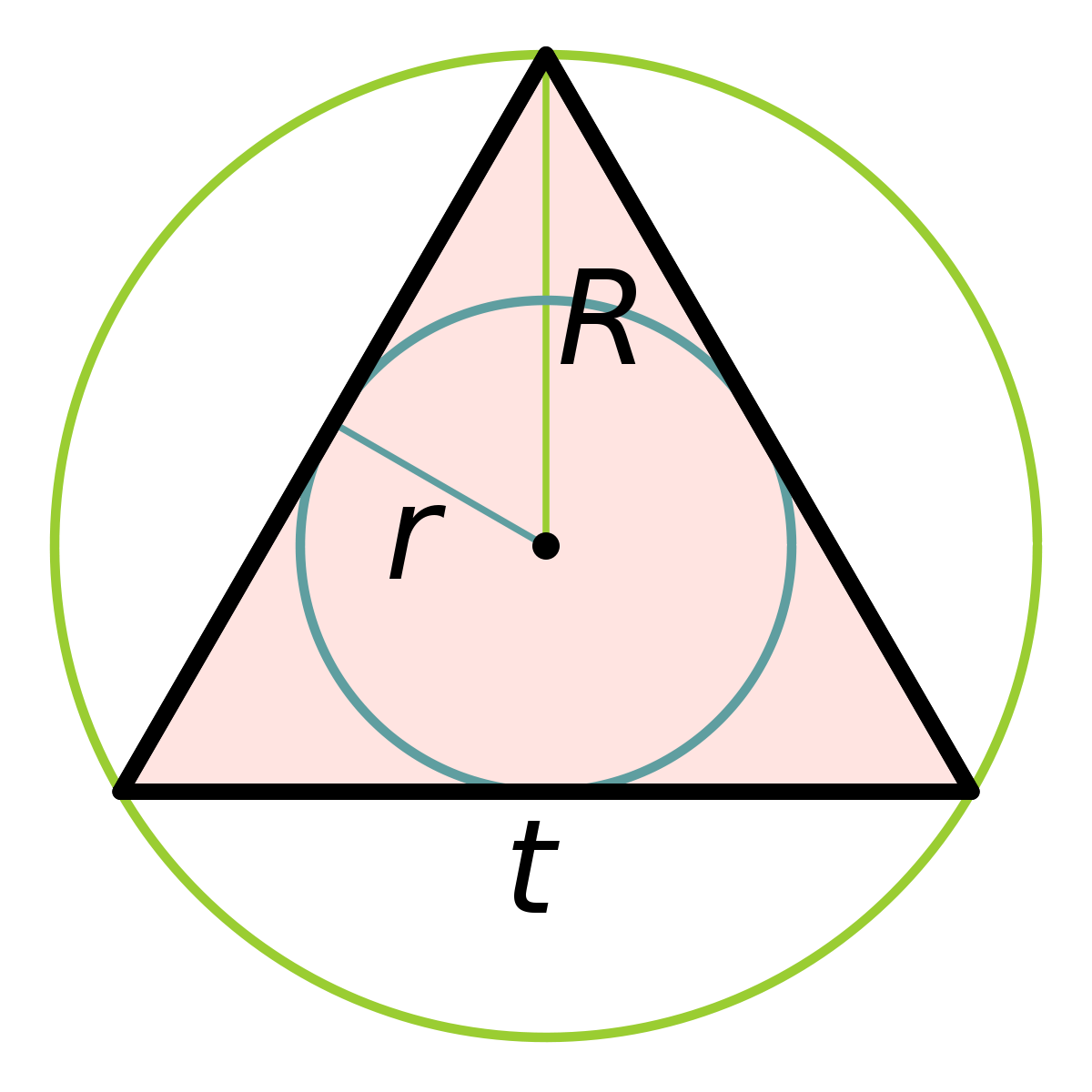
- Свойства равностороннего треугольника (правильного треугольника)
- Геометрия — сложная и увлекательная наука. Она наделяет даже самые простые фигуры несколькими дополнительными параметрами и элементами.
- Можно также определить биссектрису как геометрическое место точек внутри угла, равноудалённых от сторон этого угла [1].
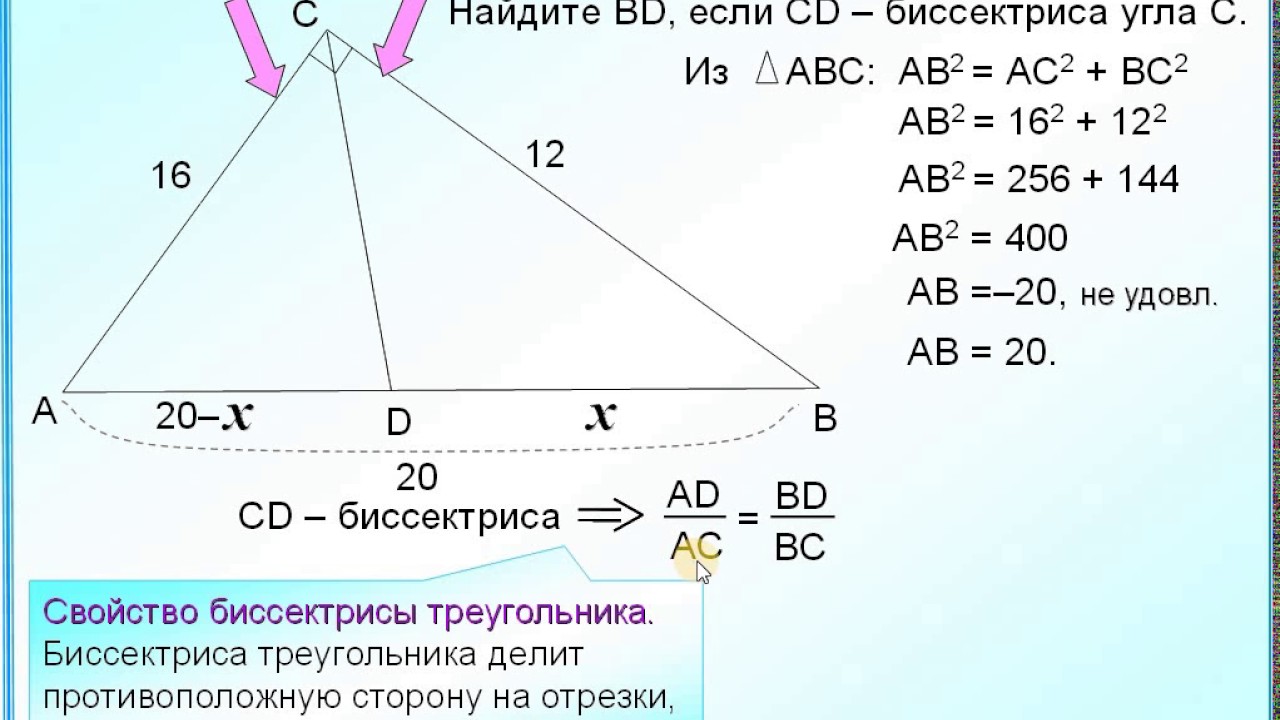
- Биссектриса треугольника делит противоположную сторону треугольника на два отрезка, длины которых пропорциональны соответствующим прилежащим сторонам треугольника. Бесплатный летний онлайн-лагерь.




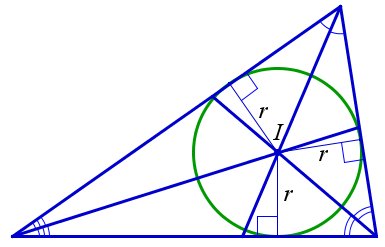

Геометрическим местом точек называется множество всех точек, обладающих определенным свойством. Например, геометрическим местом точек, расположенных по одну сторону от данной прямой и равноудаленных от нее, является прямая, параллельная данной. Все точки на данном рисунке равноудалены от прямой a и лежат по одну сторону от нее. Докажем, что биссектриса угла является геометрическим местом точек. Каждая точка биссектрисы неразвернутого угла равноудалена от сторон этого угла.




